Cum să găsiți direcțiile cosinilor unui vector
Cum să găsiți direcțiile cosinilor unui vector
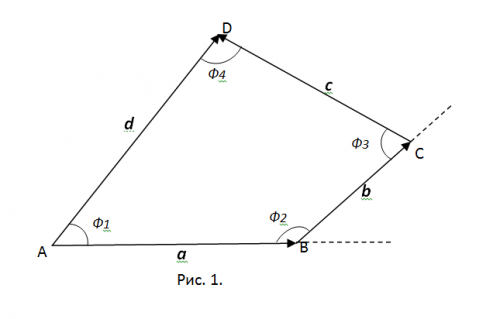
Indicați prin alfa, beta și gamma unghiurile formate de vectorul a cu direcția pozitivă a axelor de coordonate (vezi figura 1). cosinus Aceste unghiuri se numesc direcțiile cosinelor vector a.

Veți avea nevoie
- - hârtie;
- - mânerul.
instrucție
1
2
Trebuie notat de proprietatea de bază a direcționării cosinelor. Suma pătratelor direcției cosine vector este egal cu unitatea.În fapt, cos2 (alfa) + cos2 (beta) + cos2 (gamma) = a1 ^ 2 (a1 ^ 2 + a2 ^ 2 + a3 ^ 2) +2 ^ (a1 ^ 2 + a2 ^ 2 + a3 ^ 2) + a3 ^ 2 / (a1 ^ 2 + a2 ^ 2 + a3 ^ 2) + a2 ^ 2 + a3 ^ 2) = 1.
3
Prima metodă Exemplu: dat: vector a = {1, 3, 5). Găsiți cosinusele direcționale. Soluție. Conform celor găsite, vom scrie: | a | = sqrt (ax ^ 2 + ay ^ 2 + az ^ 2) = sqrt (1 + 9 +25) = sqrt (35) = 5,91. Astfel, răspunsul poate fi scris în următoarea formă: {cos (alfa), cos (beta), cos (gamma)} = {1 / sqrt (35), 3 / sqrt (35), 5 / 0,16, 0,5, 0,84}.
4
A doua modalitateCând găsiți direcțiile cosinale vector a, puteți utiliza tehnica de determinare a cosinuselor unghiurilor folosind un produs scalar. În acest caz, în minte, există unghiuri între a și direcția individului vectordreptunghiulare coordonate carteziene i, j și k. Coordonatele lor sunt {1, 0, 0}, {0, 1, 0}, respectiv {0, 0, 1}. Trebuie reamintit faptul că produsul scalar al vectorilor este definit după cum urmează. Dacă unghiul este între vectorapoi produsul scalar al celor două vânturi (îndefinitie) este un numar egal cu produsul modulilor vectorilor prin cosφ. (a, b) = | a || b | cos φ. Apoi, dacă b = i, atunci (a, i) = | a || i | cos (alfa) sau a1 = | a | cos (alfa). Mai mult, toate acțiunile sunt efectuate în același mod ca și metoda 1, ținând cont de coordonatele lui j și k.