Sfat 1: Cum se determină tipul de triunghi
Sfat 1: Cum se determină tipul de triunghi
Un triunghi este cel mai simplu dintre poligoane. Se compune din trei puncte situate într-un plan, dar nu o linie dreaptă, pereche legată de segmente. Cu toate acestea, triunghiurile pot fi destul de diferite și, ca o consecință, au proprietăți diferite.
instrucție
1
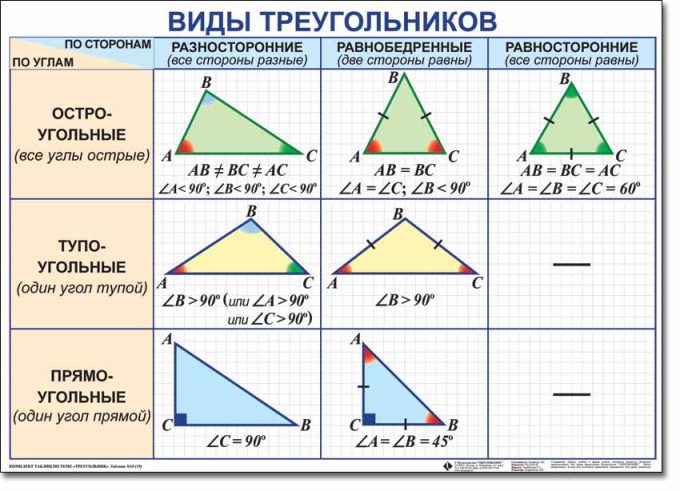
Se obișnuiește să ieșiți din șase specie triunghiuri. În centrul acestei diviziuni sunt două clasificări: la colțuri și la laturi. Clasificarea pe tipuri de unghiuri presupune împărțirea triunghiurilor în acută, rectangulară și obtuză. Clasificarea prin raportul laturilor împarte triunghiurile în versatil, echilateral și isoscele. Și fiecare triunghi aparține simultan două tipuri. De exemplu, poate fi dreptunghiulară și versatilă în același timp.
2
Definirea formularului triunghi de tipul colțurilor, fiți foarte atenți. Se va numi un triunghi obtuz, în care unul dintre colțuri este rotit, adică mai mult de 90 de grade. Un triunghi dreptunghiular poate fi calculat prin prezența unui unghi direct (egal cu 90 de grade). Cu toate acestea, pentru a clasifica triunghiul ca fiind acut, va trebui să vă asigurați că toate cele trei unghiuri sunt clare.
3
Definirea formularului triunghi prin raportul laturilor, mai întâi va trebuiaflați lungimile tuturor celor trei laturi. Cu toate acestea, dacă prin condiția lungimii laturilor nu vi se oferă, unghiurile vă pot ajuta. Versatil va fi un triunghi, toate cele trei laturi ale căror lungimi diferite. Dacă lungimile laturilor sunt necunoscute, atunci triunghiul poate fi clasificat ca versatil dacă toate cele trei unghiuri sunt diferite. Triunghiul versatil poate fi obtuz, dreptunghiular și acut.
4
Un triunghi isoscel, doi dintre eitrei laturi ale cărora sunt egale unul cu celălalt. Dacă lungimea laturilor nu vi se dă, trebuie să fiți ghidați de două unghiuri egale. triunghi isoscel ca versatil, si poate fi obtuz și în unghi ascuțit și dreptunghiular.
5
Echivalentul poate fi numit doarUn triunghi, ale cărui trei laturi au aceeași lungime. Toate unghiurile sale sunt de asemenea egale unul cu altul, și fiecare dintre ele este egal cu 60 de grade. Prin urmare, este clar că triunghiurile echilaterale sunt întotdeauna unghiuri acute.
Sfat 2: Cum să identificați un triunghi obtus și unghi ascuțit
Cel mai simplu dintre poligoane este un triunghi. Se formează prin intermediul a trei puncte situate într-un plan, dar care nu se află pe o linie dreaptă, pereche legate de segmente. Cu toate acestea, triunghiurile sunt de diferite tipuri și, prin urmare, au proprietăți diferite.

instrucție
1
Se obișnuiește să se distingă trei tipuri de triunghiuri: obtuz, acut și dreptunghiular. Aceasta este o clasificare pe tip de unghiuri. Un triunghi obtuz este unul în care unul dintre unghiuri este unghiular. Blunt este unghiul, care este mai mare de nouăzeci de grade, dar mai puțin de o sută optzeci. De exemplu, în triunghiul ABC, unghiul ABC este de 65 °, unghiul BCA este de 95 °, unghiul CAB este de 20 °. Unghiurile ABC și CAB sunt mai mici de 90 °, dar unghiul BCA este mai mare, astfel încât triunghiul este obtuz.
2
Un triunghi acut este un triunghi al căruitoate unghiurile sunt ascuțite. Un unghi ascuțit este un unghi mai mic de nouăzeci și mai mare de zero grade. De exemplu, în triunghiul ABC, unghiul ABC este de 60 °, unghiul BCA este de 70 °, unghiul CAB este de 50 °. Toate cele trei unghiuri sunt mai mici de 90 °, deci triunghiul este unghiular. Dacă știți că toate laturile triunghiului sunt egale, aceasta înseamnă că toate unghiurile sunt egale una cu cealaltă, în timp ce ele sunt egale cu șaizeci de grade. În consecință, toate unghiurile într-un astfel de triunghi sunt mai puțin de nouăzeci de grade, și de aceea un astfel de triunghi este unghiular.
3
Dacă în triunghi unul dintre unghiuri este egal cu nouăzeci de grade, aceasta înseamnă că nu se aplică tipului cu unghi larg sau tipului cu unghi ascuțit. Acesta este un triunghi în unghi drept.
4
Dacă forma triunghiului este determinată de relațiapărțile vor fi echilaterale, versatile și isosceles. Într-un triunghi echilateral, toate laturile sunt egale, iar acest lucru, după cum ați aflat, indică faptul că triunghiul este unghiular. Dacă triunghiul are doar două laturi sau laturile nu sunt egale unul cu altul, acesta poate fi obtuz, dreptunghiular și acut. Prin urmare, în aceste cazuri este necesar să se calculeze sau să se măsoare unghiurile și să se tragă concluzii, conform punctelor 1, 2 sau 3.
Sfat 3: Ce triunghiuri sunt numite egale
Egalitatea a două sau mai multe triunghiuri corespunde cazului în care toate laturile și unghiurile acestor triunghiuri sunt egale. Cu toate acestea, există o serie de criterii mai simple pentru a dovedi această egalitate.

Veți avea nevoie
- Manual de geometrie, o foaie de hârtie, un creion simplu, protractor, conducător.
instrucție
1
Deschideți manualul de geometrie de clasa a șapteaparagraful privind semnele de egalitate a triunghiurilor. Veți vedea că există o serie de caracteristici de bază care dovedesc egalitatea a două triunghiuri. Dacă două triunghiuri ale căror egalitate este verificată sunt arbitrare, atunci pentru ele există trei semne de bază ale egalității. Dacă sunt cunoscute informații suplimentare despre triunghiuri, principalele trei caracteristici sunt completate de mai multe. Aceasta se aplică, de exemplu, în cazul egalității de triunghiuri în unghi drept.
2
Citiți prima regulă despre egalitatetriunghiuri. După cum știți, vă permite să luați în considerare triunghiurile egale dacă puteți dovedi că un colț și două laturi adiacente ale celor două triunghiuri sunt egale. Pentru a înțelege modul în care funcționează această lege, trageți pe foaia de hârtie cu un protractor două unghiuri definite identic, formate din două raze care provin dintr-un punct. Măsurați rigla cu aceleași laturi din partea de sus a colțului desenat în ambele cazuri. Folosind un protractor, măsurați unghiurile celor două triunghiuri formate, asigurați-vă că ele sunt egale.
3
Pentru a nu recurge la astfel de practicimăsuri pentru înțelegerea egalității triunghiului, citiți dovada primului semn al egalității. Faptul este că fiecare regulă privind egalitatea triunghiurilor are o dovadă teoretică strictă, pur și simplu nu este convenabil să o folosești pentru a memora regulile.
4
Citiți al doilea semn al egalității de triunghiuri. El spune că două triunghiuri sunt egale în cazul, în cazul în care oricare dintre părți și două de colț adiacentă a două dintre aceste triunghiuri sunt egale. Pentru a aminti această regulă, imagina partea vopsite ale triunghiului și două adiacent la colțul ei. Imaginați-vă că lungimea laturilor unghiurilor sunt crescute treptat. În cele din urmă, se vor intersecta, formând un al treilea unghi. Această problemă mentală este important ca punctul de intersecție a laturilor care cresc mental, precum și unghiul rezultat este determinat în mod unic de către o terță parte, și cele două unghiuri adiacente acesteia.
5
Dacă nu vi se oferă informații despre colțuriapoi folosiți al treilea semn al egalității de triunghiuri. Conform acestei reguli, două triunghiuri sunt considerate egale dacă toate cele trei laturi ale uneia dintre ele sunt egale cu cele trei laturi ale celeilalte. Astfel, această regulă spune că lungimile laturilor unui triunghi determină în mod unic toate unghiurile unui triunghi și, prin urmare, determină în mod unic triunghiul.







