Sfat 1: Cum se construiește un copac al problemelor
Sfat 1: Cum se construiește un copac al problemelor
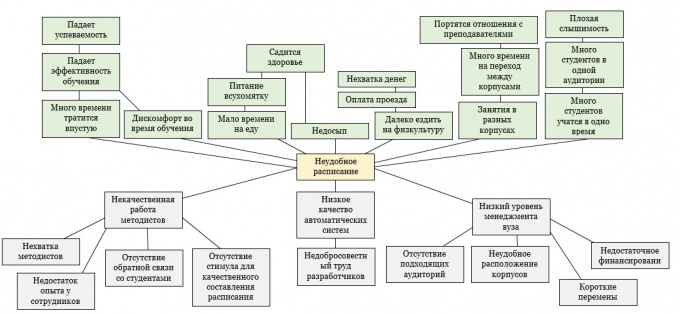
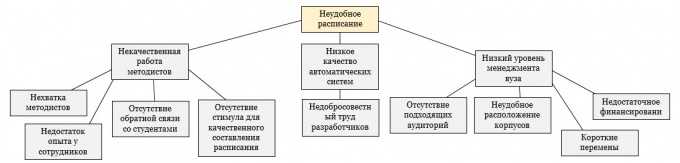
Arborele cu probleme este o cheiesă faciliteze procesul de formare a sarcinilor în întreprindere și de căutare a soluțiilor. Permite determinarea întregului spectru de cauze și consecințe interdependente ale problemei, excluzând aproape complet influența factorilor subiectivi externi. Arborele cu probleme este unul din instrumentele cheie ale analizei sistemului. Să luăm în considerare construirea acestui model pe baza unui exemplu incomod în cadrul unei universități.
instrucție
1
Formulează problema. Trebuie să existe în prezent, nu în trecut sau în viitor. Formulează în mod specific, evitând cuvinte inutile. Încearcă să atingi pe probleme globale care afectează practic imposibil ( „încălzirea globală“, „lipsa de spiritualitate în societate“ etc.).
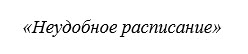
2
Faceți o listă cu părțile interesate. Adică este necesar să se identifice toți participanții care sunt afectați direct sau indirect de această problemă. Pentru aceasta trebuie să răspundeți la următoarele întrebări. Pe cine are această problemă cel mai mare impact? Cine va participa direct la soluționarea problemei? Ce organizații sau grupuri de persoane pot influența cursul de lucru? Determinați exact modul în care o persoană interesată depinde de problemă.

3
Începeți să construiți un copac al problemelor. Se compune din trei părți: rădăcini, trunchi și coroană. Rădăcinile sunt motivele care au cauzat problema. Ei sunt aceia care îi determină existența. Dacă le remediați, problema dispare. Trunchiul este formula. Crohn - toate consecințele care au cauzat această problemă. Mai întâi trage un butoi.

4
În continuare, trebuie să desenați rădăcinile. Mai întâi scrieți toate motivele care apar în sesiunea de brainstorming. Apoi grupați-i și indicați relațiile. Încercați să găsiți numărul maxim de "rădăcini", deoarece decizia lor va avea un impact decisiv.
5
Ultimul punct este coroana. Identificați punctele imediate de contact între problemă și consecințe. Apoi urmăriți ce alte impacturi negative pot avea, adică, mergeți la nivelul de mai jos. Continuați să faceți acest lucru atâta timp cât consecințele sunt încă parte a problemei.
Sfat 2: Cum se construiește o rădăcină pe un grafic
Fiecare funcție, inclusiv o funcție patratică, poate fi construită pe un grafic. Pentru a construi această imagine grafică, se calculează rădăcinile ecuației patrate date.

Veți avea nevoie
- - conducătorul;
- - un simplu creion;
- - un notebook;
- - mânerul;
- - șablon.
instrucție
1
Găsiți rădăcinile ecuației patrate. Ecuația pătratic cu o singură necunoscută, după cum urmează: AX2 + bx + c = 0. Aici x este necunoscut; Coeficienții a, b și c sunt cunoscute, în care nu trebuie să fie 0. Dacă vom împărți ambele părți ale ecuației pătratice predeterminate pentru un factor, de a primi ecuația pătratică redus de forma x2 + px + q = 0, unde p = b / a și q = c / a. Cu condiția ca unul dintre coeficienții b sau c, sau ambele sunt egale cu zero, o ecuație pătratică obținută ai numit incomplet.
2
Găsiți discernământul care este calculat deformula: b2-4ac. În cazul în care valoarea D este mai mare decât 0, ecuația patratică va avea două rădăcini reale; dacă D = 0, rădăcinile reale găsite vor fi egale una cu cealaltă; dacă D
3
Reprezentarea grafică a unei funcții patrateva fi o parabolă. Definiți date suplimentare pentru plotarea graficului acestei funcții patrate: direcția "ramurilor" parabolei, vârful ei și ecuația axei de simetrie. Dacă a> 0, atunci "ramurile" parabolei sunt îndreptate în sus (în caz contrar, "ramurile" vor fi îndreptate în jos).
4
Pentru a determina coordonatele vârfului parabolei, găsiți x după formula: -b / 2a, apoi înlocuiți valoarea "x" în ecuația patratică pentru a obține valoarea y.
5
În cele din urmă, ecuația axei de simetrie depinde devalorile coeficientului c în ecuația patratică originală. De exemplu, dacă ecuația quadratică y = x2-6x + 3, atunci axa simetriei va trece de-a lungul liniei în care x = 3.
6
Cunoscând direcția "ramurilor" parabolei, coordonatele eivârfuri, precum și axa de simetrie, construi folosind un grafic model predeterminat al ecuației pătratice. Se indică pe grafic reprezentate rădăcini: ele vor fi zero.







